1. Fancier Optimization: Adam을 쓰자
1) SGD의 문제점
2) SGD+Momentum
3) AdaGrad
4) RMSProp
5) Adam
6) Learning Rate Decay
7) First, Second-Order Optimization
2. Regularization
1) Model Ensemble
2) Dropout
3) Batch Normalization
4) Data Augmentation
5) DropConnect
6) Fractional Max Pooling
7) Stochastic Depth
3. Transfer Learning
1. Fancier Optimization
1) SGD의 문제점
① loss가 변화하는 속도가 차원마다 다르다면, gradient descent는 zigzag 형태로 비효율적이게 움직이게 된다.

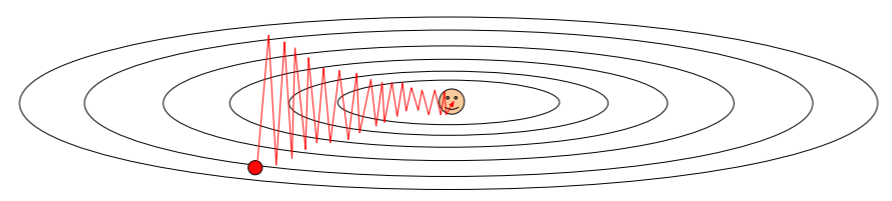
왼쪽 그림과 같은 weight 함수들이 있다. 수평축보다 수직축의 weight 변화에 더 민감하다. gradient의 update 방향이 고르지 못하기 때문에 빠르게 변화하는 수직 차원을 가로지르면서 update가 지그재그로 움직이게 된다. 차원이 더 커지고 loss가 업데이트되는 방향이 불균형하다면 SGD는 잘 작동하지 않는다고 한다.
왼쪽 그림에서 빨간 지점에서의 loss를 bad condition number로, Hessian matrix의 최대 나누기 최소 sigular values의 값의 비율이 크다(좋지 않다)는 것을 의미한다.
② local minima에 갇혀 SGD가 멈추는 경우가 생긴다.

위의 그림에서 x축이 weight, y축이 loss라고 생각해보자. 빨간 지점에서의 gradient는 0이 되기 때문에 loss가 전체적으로 봤을 때 최저 지점이 아님에도 SGD가 멈춰버린다.
③ Saddle points: loss의 update 방향이 서로를 상쇄시켜 gradient가 0이 되는 경우이다. 고차원에서는 흔하게 발생하는 일이라고 한다.
④ Loss function을 계산할 때 minibatch의 data를 가지고 실제값을 추정하기 때문에 정확한 gradient를 얻을 수 없다.
그래서,
2) SGD + Momentum

- 기존의 SGD에 "velocity"라는 개념을 넣은 것이다. 다음 step에서 gradient vector가 자신의 방향이 아닌 velocity 방향으로 움직이게 된다. velocity term이 추가되면서 기존의 SGD보다 조금 더 큰 값으로 update가 진행된다. 물리적으로 생각해봤을 때 공이 높은 위치에서 굴러내려오면 떨어지면서 속도가 점점 빨라진다. local minima에 도달해도 여전히 velocity를 가지고 있기 때문에 local minima에서 update가 멈추는 일을 방지할 수 있다. 마찬가지로, saddle points 문제도 비슷하게 해결할 수 있다고 한다.
- $\rho$: momentum의 비율, 보통 0.9 or 0.99로 설정한다고 한다.

- Nesterov Momentum은 velocity의 방향이 잘못되었을 경우, 현재 gradient 방향을 좀 더 활용할 수 있도록 해준다. velocity는 이전 gradient들의 weighted sum을 의미하며, 시간이 지날수록 오래된 gradient들은 급격하게 감소한다. velocity의 초기값은 0으로 설정한다. (No hyperparameter)
- Convex(볼록) 함수에 대한 최적화 문제에서는 뛰어나지만 Neural Network와 같은 non-convex problem에서는 성능이 보장되지 않는다.

SGD에 비해 Momentum이 더해진 파란 곡선은 비교적 수직축의 변화가 덜한 것을 볼 수 있다. 그리고 Nesterov에 해당하는 초록색 선은 일반 Momentum에 비해 overshooting이 덜한 것을 볼 수 있다.
Q. 좁고 깊은 minima가 있을 때 momentum의 velocity를 이용하면 minima를 건너뛰게 되는 것이 아닌지?
A. 보통 원하는 minima는 일반화가 잘 되는 평평한 minima임. 좁고 깊은 minima는 심한 overfitting을 불러오기 때문에 좋은 minima가 아님. momentum이 좁고 깊은 minima를 무시해버리는 것은 버그가 아니라 momentum의 좋은 특징이라 할 수 있음.
3) AdaGrad

훈련 도중 계산되는 gradients를 활용하는 방법으로, 학습 도중에 계산되는 gradient에 제곱을 해서 더해준다. 그리고 나서 update를 할 때 앞서 계산한 grad squared term을 나눈다. 빨간 박스의 1e-7은 분모가 0이되는 것을 방지하기위한 hyperparameter인데 보통 1e-7, 1e-8을 많이 쓴다고 한다.
AdaGrad의 문제점은 학습이 계속 진행될수록 step size가 줄어들어 학습 횟수가 늘어난다는 점이다. grad_squared가 학습을 진행할수록 점점 커지게 되고, 큰 값을 나누기 때문에 x가 작아지게 된다. convex problem에서는 점점 작아지는 것이 문제가 되지 않지만 non-convex problem에서는 saddle point에 갇히게 될 경우 문제가 된다.
일반적으로 Neural Network를 학습시킬때 Adagrad는 잘 사용하지 않는다고 한다.
4) RMSProp

RMSProp에서는 앞선 문제를 해결하기 위해 기존의 누적값에 decay_rate를 곱한다. decay_rate로 보통 0.9 or 0.99를 많이 사용한다고 한다. 이를 통해 step의 속도를 조절할 수 있다.

Momentum의 경우 overshoot한 뒤 원래의 minima로 돌아오지만 RMSProp은 각 차원마다 상황에 맞도록 적절하게 궤적을 수정한다.
5) Adam: RMSProp + Momentum

- first_moment: gradient의 가중합 (Momentum - velocity 담당)
- second_moment: gradient의 제곱 이용 (AdaGrad / RMSProp)
- 초기에 second_moment를 0으로 초기화했다. second_moment를 1회 업데이트했을 때, beta2(decay_rate)가 1에 가까운 값을 가지기 때문에 second_moment는 여전히 0에 가까울 것이다. 0에 가까운 값을 나눠주게 되면 초기 step이 엄청 커지는데, 이 커진 step이 실제 loss function이 가파르기 때문에 커진게 아니라 second를 0으로 초기화했기 때문에 발생한 것이므로 보정 항을 추가해준다.
- 일반적으로 Adam을 가장 많이 사용한다고 한다. (beta1 = 0.9, beta2 = 0.999, learning rate = 1e-3, 1e-4 추천)

Adam은 Momentum보다 overshoot가 덜하다. 2차원에서는 정확히 보이지 않지만 Adam은 RMSProp과 같이 각 차원의 상황을 따로 고려해서 step을 이동한다. Momentum과 RMSProp의 특징을 동시에 가지고 있다.
Adam의 문제점은 loss function이 축 방향으로 정렬되지 않고 기울어져 있 경우에, 차원에 해당하는 축만을 조절할 수 있다는 점이다. (poor conditioning)
6) Learning Rate Decay
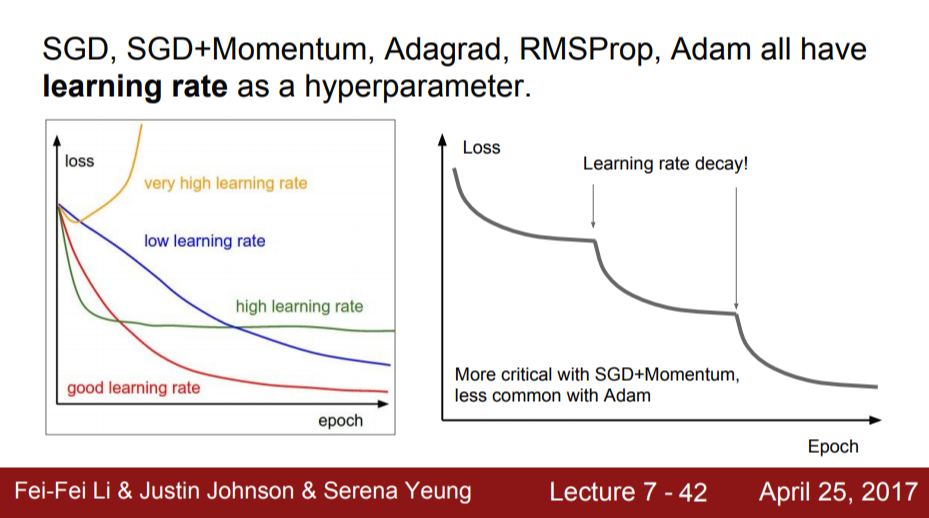
Learning Rate Decay는 초기에 Learning rate를 높게 설정하고, 학습이 진행될수록 Learning rate를 점점 낮추는 방법이다. (ex. 100,000번째 iteration에서 learning rates를 낮춤)
Exponential Decay는 학습 과정 동안에 꾸준히 Learing rate를 낮춘다.
Resnet 논문에서는 step decay learning rate 전략을 사용했다고 한다. 위의 오른쪽 그래프를 보면 gradient가 평평해지다가 갑자기 내려가는 구간이 생긴다. 이 구간이 learning rate를 낮추는 구간이다. 그렇다면 learning rate를 언제 낮춰야할까? learning rate는 수렴을 잘하고 있는 상황에서 gradient가 점점 작아지면 learning rate가 너무 높아서 깊게 들어가지 못한다. 이 때 learning rate를 낮추게 되면 속도가 줄어들 것이고 지속해서 loss가 내려갈 수 있다. Adam보다 SGD+Momentum을 사용할 때 자주 사용하는 방식이다.
일반적으로 learning rate decay는 학습 초기부터 고려하지 않는다. learning rate와 decay 등을 교차 검증하려고 하면 문제가 너무 복잡해지기 때문에 우선 decay 없이 학습을 시켜본다. 그리고 loss curve를 살펴본 후 decay가 필요한 위치가 어디인지 판단한다.
7) First, Second-Order Optimization
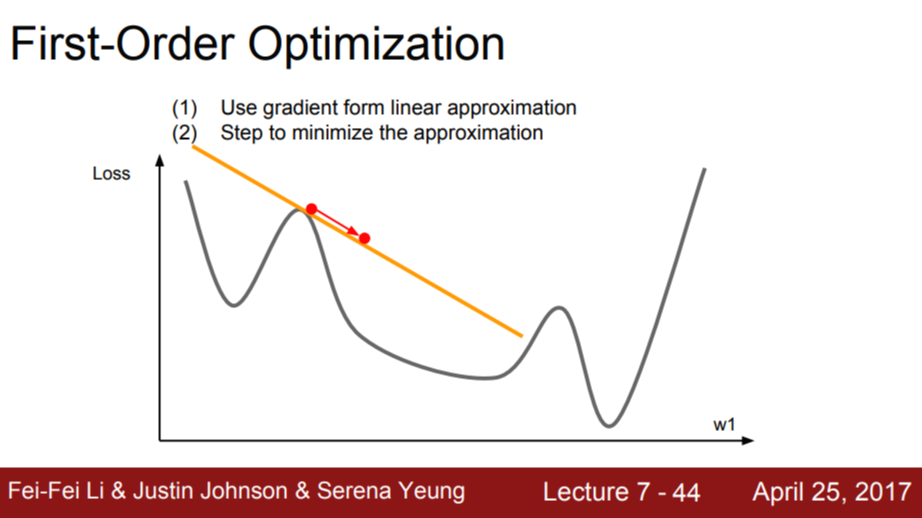
지금까지 배운 최적화 알고리즘은 모두 1차미분을 활용해 loss function을 선형 함수로 근사한 것이었다. (1차 테일러 근사)

2차 근사를 이용하면 1차 근사를 사용했을 때보다 minima에 더 빠르게 접근할 수 있다.

Newton's method: 2차 미분값들로 이루어진 Hessian Matrix H의 역행렬을 이용해 loss function의 2차 근사를 계산하고 minima에 도달한다. 이 방법에는 learning rate가 없다! 근데 실제로는 근삿값이기 때문에 필요하긴 하다고 한다.
딥러닝에서는 현실적으로 메모리에 Hessian Matrix(N by N, N: network의 parameter 수)를 저장할 수 없고 역행렬 계산도 불가능하기 때문에 사용하지 않는다고 한다.

대신에 다음과 같은 방법으로 H를 근사한다.
Quasi-Newton methods: Hessian matrix를 Low-Rank로 근사하는 방법
L-BFGS: Second-Order Optimizer. 2차 근사가 stochastic case에서 잘 동작하지 않기 때문에 DNN에서는 잘 사용하지 않는다. 그리고 non-convex 문제에도 적합하지 않다고 한다.
실제로 Optimization을 진행할 때는 Adam을 제일 많이 사용한다. 하지만 full batch update가 가능하고 stochasticity가 적은 경우 L-BFGS가 좋은 선택이 될 수도 있다. 뉴럴 네트워크 학습에 많이 쓰이지는 않지만 stochasticity와 parameter가 적은 style transfer과 같은 알고리즘에 종종 L-BFGS를 사용할 수 있다.
지금까지 training error를 줄이기 위한 최적화에 대해 다루었다. 하지만 unseen data에 대한 성능이 더 중요하다.
2. Regularization
1) Model Ensemble
여러 모델을 독립적으로 학습시켜 사용한 모델 개수의 평균치를 결과로 사용한다. 모델의 수가 늘어날 수록 overfitting이 줄어들고, 성능이 좋아진다. (보통 2% 정도 향상된다고 한다.)

tips and tricks: 여러 모델을 독립적으로 학습시키는 것이 아니라, 하나의 모델을 학습 도중 저장(snapshots)하고 앙상블로 사용할 수 있다. 그리고 test time에는 여러 snapshots에 나온 예측값들을 평균 내서 사용한다. learning rate를 엄청 낮췄다가 높혔다가를 반복해 loss function이 다양한 지역에 수렴할 수 있도록 만들어준다. 모델을 한 번만 train시켜도 좋은 성능을 얻을 수 있게 해준다.

Polyak averaing: 학습하는 동안에 parameter의 exponentially decaying average를 계속 계산한다. 학습 중인 네트워크의 smooth ensemble 효과를 얻을 수 있다. 때때로 조금의 성능 향상을 보이지만 실제로 자주 사용하지는 않는다고 한다.

우리는 단일 모델의 성능을 높이기 원한다. Regularization을 이용해 overfitting을 방지함으로써 unseen data에서의 성능을 향상할 수 있다. 앞선 강의에서 L1, L2 Regularization에 대해 다루었는데 L2 Reg는 뉴럴 네트워크에서는 잘 어울리지 않는다고 한다. 보통 뉴럴 네트워크에서는 Dropout을 많이 사용한다고 한다.
2) Dropout

forward pass의 Iteration마다 임의로 일부 뉴런의 activation function의 출력을 0으로 만든다. Dropout은 한 layer씩 진행된다. 한 layer의 출력을 전부 구하고 임의로 일부를 0으로 만든다. 그리고 다음 layer로 넘어가는 방식이다.
next_activation = prev_activation * weight.
현재 activation의 일부를 0으로 만들면 다음 layer의 일부는 0과 곱해질 것이다.
fc layer에서 흔히 사용하지만 conv layer에서도 종종 볼 수 있다. conv layer의 경우 전체 feature map에서 dropout을 시행한다. 또한 여러 channels이 있기 때문에 일부 채널 자체를 dropout 시킬 수 있다.
- 장점
- 네트워크가 일부 feature에만 의존하는 것을 방지함: 다양한 feature 골고루 이용해 overfitting을 막는 효과를 가짐
- 단일 모델로 앙상블의 효과를 가질 수 있음: dropout으로 만들 수 있는 subnetwork의 수는 다양함. 서로 파라미터를 공유하는 subnetwork 앙상블을 동시에 학습하는 것이라고 생각할 수 있음

train time에 네트워크에 randomness를 추가해 training data에 너무 fit되는 것을 막는다.
test time에는 random 값(z)을 부여하는 것은 좋지 않다. 그래서 test time에 randomness를 위의 적분식을 통해 average out시켜 generalization 효과를 주고자 한다. 하지만 이 적분을 다루는 것은 상당히 까다롭기 때문에 적분을 근사시키고자 한다.

output: a / input: x, y / weight: $w_1, w_2$라고 할 때, test time에서 a는 $w_1 x + w_2 y$이다. 앞선 ppt 장에서 dropout probability(p)를 0.5로 설정했다. dropout이 될 수 있는 모든 상황을 고려해 기댓값을 구하면 $\frac{1}{2} ( w_1 x + w_2 y) $가 나온다.
train time의 기댓값이 test time의 절반이다. dropout probability를 test time network의 출력에 곱해서 둘의 기댓값을 같게 만들 수 있다.


Inverted Dropout: test time에는 계산 효율이 중요하다. 곱하기 연산이 하나 추가되는 것도 신경쓰이는 일이다. 그래서 test time에는 기존 연산을 그대로 사용하고, train time에 p를 나눠준다.
Q. Dropout을 사용하게 되면 train time에서 gradient에 어떤 일이 일어나는가?
: Dropout이 0이 되지 않는 노드에서만 Backprop이 발생하기 때문에 dropout을 사용하게 되면 step마다 업데이트되는 파라미터 수가 줄어들고, 전체 학습시간이 늘어난다. 대신 모델이 수렴한 후에는 더 좋은 일반화 능력을 얻을 수 있다.
3) Batch Normalization
train time: mini batch로 하나의 데이터가 샘플링 될 때 매번 서로 다른 데이터들과 만나게 된다. 각 데이터를 얼마나, 어떻게 regularization 시킬 것인지에 대한 stochasticity가 존재한다.
test time: regularization을 mini-batch 단위가 아닌 global 단위로 수행함으로써 stochasticity를 평균화 시킨다.
bn은 dropout과 유사한 regularization 효과를 가진다. 그래서 실제로 bn을 사용할 때는 dropout을 사용하지 않는다고 한다.
4) Data Augmentation

train time에 label은 그대로 유지한 채 이미지를 무작위로 변환한다. (horizontal flips, crop, color jittering ...)

test time: stochasticity를 average out함.
"네 개의 각 코너"와 "중앙"에서 잘라낸 이미지와 이들의 "반전 이미지"를 사용한다.
5) DropConnect
Dropout과 유사한 방법. activation function이 아닌 weight matrix를 임의적으로 0으로 만들어주는 방법이다.
6) Fractional max pooling
training time에 pooling 연산을 수행할 지역을 임의로 선정한다. 그리고 test time에 stochasticity를 average out 시기키 위해 pooling regions를 고정시키거나 여러 개의 pooling regions을 만들고 averaging over 시킨다.
7) Stochastic depth

train time: 네트워크의 layer를 randomly drop한다. layer 중 일부를 제거해 버리고 일부만 사용해서 학습을 진행한다.
test time: 전체 네트워크를 다 사용한다.
3. Transfer Learning
가지고 있는 데이터 세트가 적을 때 쓸 수 있는 방법. 아주 보편적임!!!
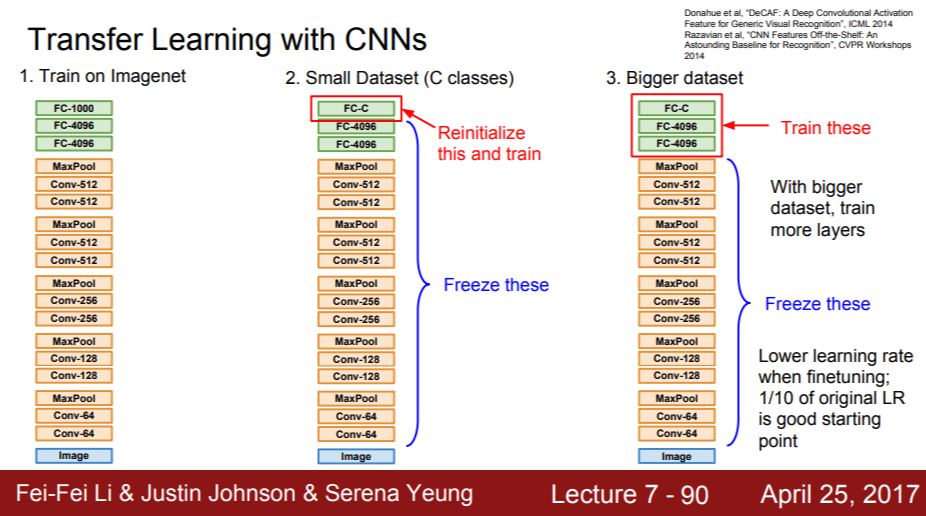
① ImageNet과 같은 아주 큰 데이터셋을 CNN에 한번 학습 시킴
② 학습된 features를 우리가 가진 작은 데이터 세트에 적용하고자 함
ex) 1000개의 ImageNet category → C(10)종의 강아지를 분류. 데이터가 엄청 적음
③ 일반적으로 가장 마지막의 fc layer는 최종 feature와 class score간의 연결인데 이를 초기화 시켜줌 (가중치 행렬 초기화)
ex) 4,096 x 1000 → 4,096 x C(10)
④ 나머지 이전의 모든 layer들의 가중치 freeze
→ linear classifier를 학습시키는 것과 같음. 오로지 마지막 layer만 가지고 데이터를 학습시키는 것. 아주 작은 데이터 세트일지라도 아주 잘 작동하는 모델을 만들 수 있음.

ⓐ 적은 양의, 유사한 데이터: 기존 모델의 top layer만 학습
ⓑ 조금 더 많은 양의, 유사한 데이터: 모델 전체를 fine tuning
ⓒ 적은 양의, 다른 데이터: 기존 모델이 안 통할 수 있음
ⓓ 조금 더 많은 양의, 다른 데이터: 많은 layer들을 fine tuning
'cs231n' 카테고리의 다른 글
| lec6. Training Neural Networks, Part I (0) | 2021.07.09 |
|---|---|
| lec5. Convolutional Neural Networks (0) | 2021.07.08 |
| lec4. Backpropagation & Neural Networks (0) | 2021.07.08 |
| lec3. Loss Functions & Optimization (0) | 2021.07.08 |
| lec2. Image Classification (0) | 2021.07.08 |




댓글