lec4. Backpropagation & Neural Networks
★ 1. Backpropagation
2. Neural Networks
1. Backpropagation
- Computational Graphs는 이렇게 생겼다. 예시다.

1) Backpropagation: Upstream Gradient x Local Gradient

[Simple Example]
- $ f(x,y,z) = (x+y)z $
- $ x=-2, y=5, z=-4 $
- want to know $ \frac{ \delta f }{ \delta x}, \frac{ \delta f }{ \delta y}, \frac{ \delta f }{ \delta z} $
① local gradient를 구한다.


② Upstream Gradient와 Local Gradient를 곱한다.

[Another Example]
- $ f(W, x) = \frac{1}{1+{e}^{-(w_{0}x_{0}+w_{1}x_{1}+w_{2})}} $
- $ w_{0}=2, x_{0}=1, w_{1} = -3, x_{1} =-2, w_{2} = -3 $

- Patterns in backward flow
① add gate: gradient distributor, upstream gradient가 그대로 전달
② max gate: gradient router, forward pass에서 값이 큰 쪽으로 gradient 몰빵, 다른 쪽은 0

③ mul gate: gradient switcher, (upstream gradient) x (반대 편의 forward pass 값)
2) Vectorized Operations
- Gradients for vectorized code
- Jacobian matrix: 다변수벡터의 도함수 행렬, 결과값 벡터에서 차원별로 편미분을 모두 구함

- Vectorized Operations

* 강의에서 나온 질문들
ⓛ What is the size of the Jacobian matrix? (4096 x 4096)
: 전체 minibatch를 한번에 다룸. 예를 들어, 100이라 치면 Jacobian matrix는 409,600 x 409,600 matrix 크기를 가짐
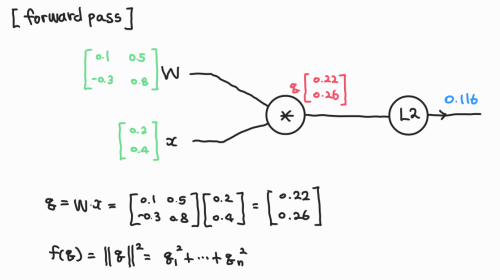
② What does it look like?
- $ f(x, W) = {|| W \cdot x ||}^2 = \sum_{i=1}^n {(W \cdot x)}^2 $
- $ x \in {R}^n, W \in {R}^n $


2. Neural Networks
(Before) Linear Score function: $ f = W_1x $
(Now) 2-layer Neural Network: $ f = W_2 \max (0, W_1x) $
3-layer Neural Network: $ f = W_3 \max (0, W_2 \max (0, W_1x)) $
...
n-layer Neural Network


1) Activation Functions

2) Neural Networks

# forward-pass of a 3-layer neural network:
f = lambda x: 1.0/(1.0 + np.exp(-x)) # activation function: sigmoid
x = np.random.randn(3, 1) # random input vector of three numbers (3x1)
h1 = f(np.dot(W1,x) + b1) # calculate first hidden layer activations (4x1)
h2 = f(np.dot(W2,h1) + b2) # calcuate second hidden layer activations (4x1)
out = np.dot(W3, h2) + b3 # output neuron (1x1)