Basic Concepts
- 원하는 데이터의 검색속도를 향상시키기 위한 메커니즘
- Search Key: column 1개 or column들의 합성
- index file: index entries로 구성됨
- index entries: (search-key, pointer) 형태의 레코드
- 인덱스 파일 크기 <<<<<<<< 원래 파일 크기
- 인덱스 파일은 메인 메모리 버퍼에 계속해서 올려놓을 수 있을 정도로 작음
- 인덱스의 두 가지 종류
- Ordered indices: search key가 순서대로 정렬
- Hash indices
- search key가 hash function을 통해 bucket 번호로 바뀜
- 인덱스 엔트리는 버컷들에 균등하게 분포되어 있음
Index Evaluation Metrics
- 검색 타입
- Access time
- 삽입/삭제 시간
- Space overhead
Ordered Indices
- 인덱스 엔트리들이 search key를 기준으로 정렬되어 있음
- Clustering index (or primary index)
- 파일 레코드 순서 = 인덱스 search key 순서
- Non-clustering index (or secondary index)
- 파일 레코드 순서 ≠ 인덱스 search key 순서
- Index-sequential file
- 인덱스된 순차 파일
- search key로 정렬된 순차 파일인데, 그 search key에 대해 clustering index가 설정되어 있어야 함
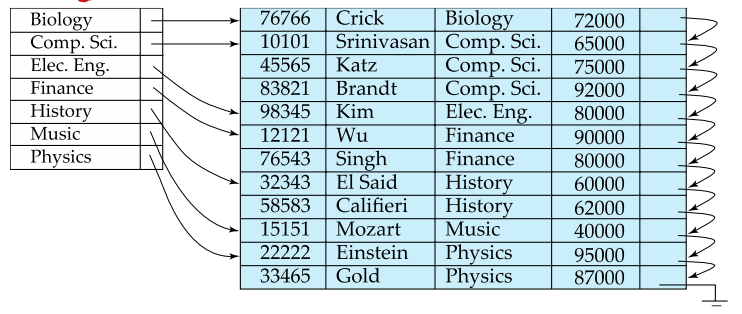
Dense Index Files
- 모든 search-key에 대응하는 레코드가 존재해야 함
- non-clustering index는 반드시 dense 해야 함
Sparse Index Files
- 레코드 값이 너무 많아서 dense하게 만들면 인덱스의 사이즈가 너무 커짐 → 일부만 index로 설정
- 레코드가 search-key에 대해 순차적으로 정렬되어 있을 때 이용 가능
- dense index와 비교했을 때,
- 공간 차지가 덜 해, db 업데이트에 대한 유지부담 ↓
- 그러나, 부분적인 순차접근을 요구하기 때문에 검색성능이 조금 떨어짐
Clustering vs Non-clustering
- 인덱스는 검색성능을 향상 시키지만
- db 업데이트, column 수정, record 값의 삽입/삭제에 대한 부담이 있음
- clustering index: 원하는 레코드가 cluster 되어있기 때문에 disk I/O ↓
- Non-clustering index: 레코드들이 흩어져 있기 때문에 disk I/O ↑
Multilevel Index
- 인덱스를 위한 인덱스
- 인덱스 크기가 커질 수 있음
- 인덱스 접근에도 IO가 생길 수 있다
- 인덱스 자체를 데이터로 생각해 sparse한 인덱스를 만드는 방식
- outer index: sparse index of the basic index
- inner index: the basic index file
- outer index가 커지면 또 다른 레벨의 인덱스를 생성 가능
B+ Tree Index Files
- indexed-sequential file의 단점
- file size가 커짐에 따라, overflow block이 생성되어 성능이 저하됨
- 주기적으로 전체 파일을 재구성해야함
- B+ tree index의 장점
- 테이블에 레코드 삽입/삭제 시, index 유지 부담이 적음
- 전체 파일 재구성 안해도 됨
- B+ tree index의 단점
- 삽입/삭제 overhead, 공감부담이 여전히 있음
B+ Tree Index files
- 균형트리: root에서 leaf까지 높이가 같음
- 인덱스가 disk에 저장됨
- 공간 사용 조건
- internal node: [[n/2], n]개의 자식을 가져야 함
- n: 각 node가 가질 수 있는 최대 자식노드 수
- leaf node는 [[(n-1)/2], (n-1)]개의 값을 가짐
- e.g. n=4
- leaf node는 최소 2개, 최대 3개의 값을 가져야 함
- root node
- leaf node가 아닐 때, 최소 2개의 자식을 가져야 함
- leaf node면 [0, (n-1)]개의 값을 가질 수 있음
B+ Tree Node Structure
| P1 |
K1 |
P2 |
... |
Pn-1 |
Kn-1 |
Pn |
- P: 포인터
- leaf node: 레코드를 가리킴
- non-leaf: 자식노드를 가리킴
- K: search-key
Leaf Nodes in B+ Trees
- P1, ... Pn-1: 레코드를 가리킴
- Pn: 형제 노드를 가리킴
Non-Leaf Nodes in B+ Trees
| P1 |
K1 |
P2 |
... |
Pn-1 |
Kn-1 |
Pn |
- (P1이 가리키는 node의 search key들) < K1
- K1 <= (P2가 가리키는 node의 search key들)
Observations about B+ tree
- node들은 포인터로 연결되어 있기 때문에 논리적으로 근접한 block들이 물리적으로는 근접하지 않을 수 있음
- 부모, 자식, 형제노드가 disk 상에서는 멀리 떨어져 있을 수도 있음
- non-leaf node들은 multi-level sparse index를 구성
- B+ tree는 높이가 그렇게 높지 않다
- 최악의 경우: 각 node가 공간의 절반을 채워야하는 요건을 최소로 채우는 경우
- 높이 상한선: $[log_{[n/2]}(K)]$
- 보통 2~4임
- K: search key의 수
- n: branch factor (fanout)
- tree에서 node들이 자식을 얼마나 분기하는가
- 레코드 삽입 삭제시, index는 log time 내에 재구성될 수 있음
Queries on B+tree
- root에서 시작해서 leaf node에서 탐색 종료
- range query를 잘 지원함
- B+ tree의 성능은 B+ tree의 높이가 좌우함
Updates on B+ Tree: Insertion
- pr: 레코드를 가리키는 포인터
- v: 레코드의 search key
- v를 가지고 root 노드에서 leaf까지 검색
- 적절한 위치의 leaf node를 찾고, 빈 공간이 있으면 거기 삽입 후 종료
- 빈 공간이 없으면 leaf node를 분할해야 함
- leaf node 분할 방법
- leaf node에는 최대 (n-1)개의 search-key 값이 올 수 있음 → n 개면 overflow 발생
- new node를 만들고 2개의 node에 search-key를 정렬 순서대로 n/2개씩으로 나눔
- 새롭게 추가된 노드를 부모 노드의 자식으로 추가시켜야 함
- 부모 노드에서 overflow가 난 원래의 node를 가리키는 ptr 옆에 (search-key, ptr) 삽입
- 부모 노드에도 공간이 없다면, 또 분할 진행
- non-leaf node 분할
- 빈 공간이 없는 node N에 (k,p)를 추가시키려 함
- N을 정상 노드보다 큰 memory 상의 임시 버퍼인 M에 복사
- (k,p)를 M에다 삽입
- p1, k1, ..., k_[(n+1)/2]-1, p_[(n+1)/2]까지 N에 복사
- p_[(n+1)/2]+1, ..., p_(n+1)를 새로 할당한 node인 N'에 복사
- (k_[(n+1)/2], N')를 N의 부모 노드에 삽입
- 최악의 경우: root 분할 → 새로운 root가 생기고, tree의 높이가 1 증가함
Updates on B+ Tree: Deletion
- 테이블에서 레코드 삭제 시, 해당 (pr, v)를 leaf node에서 삭제
- merge siblings: 삭제 되었을 때, 공간 요건을 충족하지 못하면 형제 노드와 합쳐야함
- 합칠 때는 왼쪽 형제로 몰아줌
- 부모 엔트리에서 (k_(i-1), p_i) 삭제
- redistribute pointers: 형제 노드가 underflow난 node를 받아줄 공간이 없을 때, 형제 노드로부터 값 재분배
- 부모 레벨 삭제 → 재귀적으로 root까지 갈 수 있음
- 최악의 경우: root에 자식이 하나만 남으면 하나의 자식이 새로운 root가 되고, tree의 높이가 1 감소함
Complexity of Updates
- 최악의 경우: $O(log_{[n/2]}(K))$
- 실제 상황에서는 대부분 leaf node에서 끝남
- 삽입/삭제 시 전체 tree의 일부분에만 영향을 미침
Non-Unique Search Keys
- search key가 unique하지 못할 때,
- 중간 단계에 bucket을 둠
- b+ tree의 leaf node의 레코드 포인터로 list를 둠
- search key를 unique 하게 만들자
- primary key uniqufier를 합성해서 search key를 unique하게 만듦
- 단점: 공간 사용 ↑
- 장점: 삽입, 삭제 효율 ↑
B+ tree File Organization
- leaf node가 저장하는 내용: 레코드 자체
- data record들이 cluster된 채로 정렬 상태 유지
- leaf node는 절반이상이 차야함
- 레코드 포인터 수 > 레코드 저장 수
- 테이블 레코드의 삽입 삭제 = b+ tree 삽입 삭제
- B* tree: node 당 2/3 이상 full
Other Issues in Indexing
- 레코드 재할당과 non-clustering index
- 레코드가 이동하면 이동한 레코드를 가리키던 pointer가 다 업데이트 되어야 함
- b+tree file 구조에서 노드 분할은 cost가 세다
- solution: secondary index가 레코드 포인터를 저장해야하는데 pointer 대신 b+ tree file 구조를 구성하는 search-key를 대신 저장
- 비집중 인덱스를 사용해서 질의처리할때 비용이 올라가지만, clustered index 부분에서 node 분할할 때 처리 부담이 적음
B-tree Index Files
- non-leaf node에서도 레코드 연결
- 장점: leaf node까지 가지 않아도 탐색이 종료될 수 있음
- 단점
- 구현이 어려움
- non-leaf node가 가질 수 있는 자식 수 ↓, 트리 높이↑
- range query에 취약
- leaf node split에서 b+ tree와 차이점?
- overflow 발생시, 중간값이 부모노드로 올라감 (분할 값이 leafnode에 남지 않음)
Hashing
- 1 bucket = 1 disk block
- 해시함수가 레코드를 저장할 bucket 주소를 계산함
- bucket 내의 모든 레코드들을 순차적으로 점검해야함
- hash index: 레코드는 힙에, 포인터는 버킷에!
- hash file-organization: 버킷에 레코드 저장
Handling of Bucket Overflows
- bucket overflow
- 불충분한 buckets
- 불균등한 레코드의 분포
- Overflow chaining, closed address, open hashing
- 기존 파일 공간 최대한 활용
- overflow 발생시, bucket에 새로운 공간을 만들어 연결
- chaining이 많이 생기면 검색 시간복잡도가 O(n)이 됨
- static hashing 문제점
- db는 성장하고 수축함. 이 변화에 잘 적응하지 못함
- bucket이 작은데 삽입이 계속 발생하면 overflow가 많이 생기고 검색 성능이 저하됨
- 그렇다고 첨부터 크게 할당하면 공간낭비가 심함
- 해결책
- 새로운 해시함수를 가지고 재배치 → cost가 세고, normal operation을 방해함
- 동적해싱기법, 파일의 재구성
- dynamic hashing
- 주기적으로 rehashing
- hash table 내의 엔트리 수가 기존의 1.5배가 되면,
- 전체 hash table 크기를 기존의 2배짜리로 늘림
- 그리고 다시 rehashing
- cost ↑
- linear hashing
- extendable hashing
- 파일 재구성을 하지 않고 dynamic하게 유지
Multiple-Key Access
- create index dept_name_idx on instructor(dept_name)
- create index salary_idx on instructor(salary)
- create index dept_salary_idx on instructor(dept_name, salary)
- drop index salary_idx
- primary key에 대해 db 시스템이 사용자가 index를 만들지 않아도 자동으로 생성해줌
- 질의 검색 성능 향상, insert문 성능 향상
- 어떤 db에서는 외래키에 대해서도 index 생성해줌
- create unique index
- search-key가 고유식별성을 가지는 후보키. 사용자가 중복되는 값을 삽입하려하면 오류 처리
Indices on Multiple Keys
- 여러 개의 column으로 이루어진 search-key
- 중복 값이 존재하는 column으로 index 생성 시,
- db 시스템이 내부적으로 uniquifier ID를 갖다붙여서 합성키에 대한 index를 생성함
- e.g. 'name': 동명이인 존재 → 시스템 내부적으로 ('name', 'id')로 index를 생성함
Bitmap Indices
- 테이블 레코드에 번호 부여
- 레코드 검색 체계가 뒷받침되어야 bitmap index 사용 가능
- 서로 다른 값의 수가 많지 않을 때 사용함
- e.g. gender, country, state, ...

- 삽입 시
- 맨 뒤에 append
- 삭제된 레코드 위치에 삽입
- 삭제 시
- bit 수를 줄이는 것 부담스러워서 냅둠
- 대신 Existence bitmap 유지: 유효한 값의 위치를 나타냄
- multiple attributes에 대한 질의에 효율적
- 남자면서 l1 구간에 있는 사람
- m: 100110 and l1: 110011 = 100010
- 0, 4번째 사람
- 수를 세는 것도 빠름
- 매우 적은 공간 차지
- 레코드 수: n
- 레코드 사이즈: 100 bytes
- 테이블 크기: 800n bits
- bitmap index는 레코드 수만큼의 bit를 가짐
- n/800n = 1/800
- 테이블이 사용하는 공간의 1/800 차지





댓글